Dose linearity/proportionality 간단정리
약물을 개발 할 때 PK parameter의 dose linearity가 보이게 되면 "linear pharmacokineitcs"라고 하며 SAD, MAD study로 확인하고있습니다.
약물의 exposure만큼 약물의 effect가 증가한다는 의미가 되어 exposure-response relationship이나 dose selection을 support하는 근거가 됩니다. 또한, \( CL=Dose/AUC \) 이기 때문에 dose linearity는 clearance 의 constancy를 결정할 수 있는 중요한 요소이므로 precision dosing을 결정 하는 근거가 됩니다.
Dose Proportionality? Dose Linearity? :
dose proportionality를 매우 간단하게 말하자면,
약물의 농도가 용량에 비례한다면 dose proportionality가 보인다고 합니다.
$$ C\propto dose$$
$$ C=\alpha \, dose$$
하지만 concentration값은 시간에 따라 변하기 때문에
이를 대표하는 값인 AUC와 Cmax를 C의 자리에 사용하게 됩니다.
그럼 dose linearity는 뭘까요? 매우 간단한 의미로는 다음의 관계가 성립하면 됩니다.
$$ C=\alpha _{0}+\alpha \, dose$$
\( \alpha _{0}\)가 있기 때문에 비교적 proportionality보다는 유연한 조건이 되겠네요.
즉, dose가 0일 때
concentration이 0이되어야하는것이 proportionality
concentration값이 \( \alpha _{0}\) 경우(0포함)가 linearity라고 할 수 있습니다.
보통 endogenous compund인 경우 0이 아닌 경우가 많습니다.
Dose Nonlinearity :
약물은 원래 dose nonlinearity가 기본적인 베이스 입니다.
다만 특정 dose구간에서 linearity를 보이는 경우가 존재하며, 우리는 이를 찾아 활용하고 싶은거죠.
nonlinearity는 PK(ADME)전반에서 발생할 수 있으며, 대부분 absorption에 의해서 발생하고 있습니다.
nonlinearity의 조건은 다양하지만 metabolizing enzyme이나 transporter 등 system에서의 saturation이나 낮은 수용성, SR제제 등 때문에 발생합니다.
Nonlinearity는 safty와 efficacy에 영향을 미치게 됩니다.
먼저 dose-dependent absorption의 예시 중 high dose을 투여 할 경우 흡수율이 감소하는 경우에는
일반적으로 비례값보다 작은 drug concentration을 보이게 됩니다. 이렇게 되는 경우 efficacy에 영향을 주게 되구요.
그렇다면 saturable elimination인 경우는 어떨까요? 이 경우엔 high dose를 투여하는 경우 비례값보다 큰 concentration을 확인 할 수 있게 됩니다. concentration이 올라가는 경우 toxicity의 risk가 높아지기 때문에 주의해야 하구요.
이런 이유로 therapeutic window가 좁은 약물은 더 세심히 보아야 합니다.
How to evaluate dose linearity? :
그렇다면 어떻게 dose linearirty를 평가할까요?
대표적인 세 방법을 알아보도록 하겠습니다.
1. Descriptive Analysis
Descriptive Analysis의 경우에는 Dose별 PK parameter을 Dose normalization하여 수평으로 보이는지 보는 방법입니다.
만약 dose normalization 하지 않는다면, 그래프가 수평을 이루다 올라가는 양상을 보이겠죠?

통계학적으로는 ANOVA분석을 통해 parameter를 비교하는데,
$$ H_{0}:\frac{AUC_{dose1}}{Dose1}=\frac{AUC_{dose2}}{Dose2}=\frac{AUC_{dose3}}{Dose3} $$
이 때 H0이 기각이 된다면, dose proportionality에 대한 증거가 없다는 의미가 되겠죠.
2. Discrete Model
Discrete Model에서는 위와 비슷하게 Dose 별 PK parameter dose noramlization하지만 log변환하여 linear 한지 보게 됩니다.

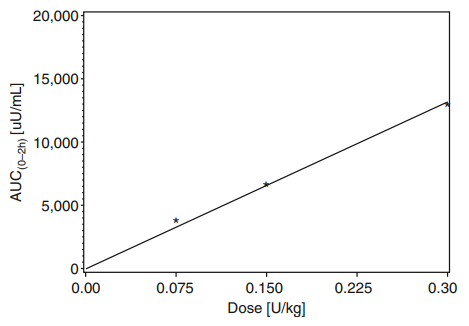
Dose의 비율만큼 PK parameter의 비율이 증가하는가를 짝을 이루어 비교를 하며,
dose normalizae된 PK parameter가 1인지를 확인하게 됩니다.
3. Power Model
Power model은 가장 대중적으로 쓰이는 모델로, Confidence Interval과 함께 제시합니다.
C를 exposure과 관련된 PK parameter인 AUC와 Cmax라고 하였을 때, power model은 다음과 같습니다.
$$ C=\alpha \, dose^{\beta}$$
\( \beta \)가 1이라면 이상적인 dose proportionality인 \( C=\alpha \, dose \)가 성립이 됩니다.
$$ C=\alpha \, dose \times dose^{\beta-1}$$
$$ C/dose=\alpha \, dose^{\beta-1}$$
\( \beta \)가 1보다 크다면 exposure가 비례값보다 크다는 의미이며,
반대로 1보다 작다면 비례값보다 작은 의미로 해석 할 수 있습니다.
즉, 각 dose를 d라고 할 때 \( d^{\beta-1}\) 은 최초 용량과 용량 d만큼의 dose normalized ratio라고 볼 수 있겟죠.
따라서 명확한 해석을 위하여 d의 range가 충분히 clinically relvant 가 커야합니다.
통계학적으로 proportional한지 확인하기 위하여 log변환을 한 후 log(C)를 simple linear model로 확인하게 됩니다.
$$ log(C)=log( \alpha)+ \beta \times log(dose)+ Error \, (for dose >0) $$
주어진 dose ratio를 통하여 deviation factor인 \( d^{\beta-1}\) 가 계산이 되고 linear model로 \( \beta \)값이 추정이 가능합니다.
이 변수를 가지고 BE와 같은 방식으로 확인을 하게 되죠.
보통 BE를 볼 때 0.8-1.25의 범위를 사용하는데, \( \beta \)의 값이 이 범위안에 들어가면 dose proportionality로 보게 됩니다.
dose proportionality를 확인할 때 기본적인 concept은 세가지 방법이 동일합니다.
dose normalize를 한 PK parameter가 일정한가? 를 확인을 하는 방법이라고 생각하시면 좀 더 쉽게 접근할 수 있을것 같습니다.
Reference
1. Eisenblaetter, T., Teichert, L. (2011). Dose Linearity and Proportionality. In: Vogel, H.G., Maas, J., Gebauer, A. (eds) Drug Discovery and Evaluation: Methods in Clinical Pharmacology. Springer, Berlin, Heidelberg.
2. https://www.certara.com/knowledge-base/why-should-you-evaluate-dose-proportionality/